Die Zuse Z4 ist einer der ältesten Computer der Welt. 1942 hat Konrad Zuse mit ihrem Bau begonnen, bis heute füllt sie einen ganzen Raum. Der Rechner nutzt Magnetbänder als Datenspeicher und hat sich aus seinem Vorgängermodell Z3 entwickelt. Er besitzt eine programmierbare Einheit zur Durchführung von Gleitkommarechnungen in den Grundrechnungsarten, die Eingabe erfolgt dabei via Lochstreifen über eine Spezialtastatur mit Zifferntasten samt Exponenten, das Komma muss relativ zu den Dezimalzahlen eingestellt werden; ausgegeben wird das Ergebnis anschließend über die Lampen des Rechenwerks.
Die vier Rechner der Z-Familie verfügen allesamt über ähnliche Architekturen. Neun Jahre bevor John von Neumann die Vorteile der Trennung von Steuerwerk, Speicher und Daten erkannte, definierte Konrad Zuse sie als notwendige Voraussetzung. Erste Überlegungen dazu äußerte er in einer Tagebuchnotiz von 1935, mit der er zugleich die Minima Moralia für seine späteren Prototypen festlegte: Für sie gilt, dass das Resultat einer exakt formulierten Rechenanweisung als Abfolge von Einzelschritten verarbeitet werden kann, die dafür nötigen Operationen werden selbsttätig und in sequenzieller Abfolge ausgeführt. Um Zwischenresultate weiterzuverarbeiten, braucht es zwei Wählwerke – eines für den Programmspeicher und eines für den Arbeitsspeicher. Die dahingehenden Anweisungen finden sich nebst Rechenoperation auf einem Lochstreifen und werden in Zeilen und Spalten dargestellt; avant la lettre findet Konrad Zuse sich im weiten Feld jener Aufschreibesysteme wieder, die im Fall der Z-Computer aus distinkten Elementen einer formalen Sprache bestehen.

Die Z4 im Deutschen Museum in München (Bild: Clemens Pfeiffer (CC BY 2.5))
Bereits die auf die Bewältigung binärer Rechenoperationen beschränkte Z1 operierte auf Basis mechanischer Schaltglieder, die Z4 verfügt schon über knapp 2200 Relais. Ihr Zusammenspiel zählt zu den physikalischen Voraussetzungen für das Funktionieren – und lieferte Zuse erste Anhaltspunkte für den Aufbau seiner Programmiersprache: Jedes der Schaltglieder im Inneren seiner Maschine kennt zwei Zustände, ruhend oder aktiv. Wenn Strom fließt, schließt sich der Bügel und der Kontakt arbeitet; geschieht dies nicht, ist der Kontakt unterbrochen und das Schaltglied inaktiv. Beide Möglichkeiten lassen sich mithilfe von zweiwertigen Logiken formalisieren. Infolgedessen können zwei Relais als Konjunktion im Sinne eines logischen UND (∧), als Disjunktion im Sinne eines logischen ODER (∨) sowie durch eine Negation (NOT, ¬ ), die einen oder beide Eingänge betrifft, interagieren. Zuses »Bedingungskom-binatorik« ist somit identisch mit den Verknüpfungen des aussagen-logischen Kalküls – quod erat demonstrandum.
Alfred Tarskis »Einführung in die mathematische Logik« von 1937 lieferte Zuse die Grundlage für die Konstruktion und Programmierung seiner Maschinen – gleichermaßen. Über das Werk des polnischen Mathematikers äußerte er sich stets wohlwollend, die dahinter stehenden Konzepte interessierten ihn jedoch nur soweit, wie sie ihm für sein konkretes Vorhaben dienlich sein konnten; demgemäß bezieht Zuse sich kaum auf die logischen Konzepte Ludwig Wittgensteins oder Kurt Gödels, auch den von Rudolf Carnap und Ernst Schröder formulierten Beiträgen dazu konnte er nur wenig abgewinnen. Anfangs arbeitete er ausschließlich mit zweiwertigen Logiken, später erweiterte er diese um Ansätze aus der Prädikaten- und der relationalen Logik. Existenzquantoren (»mindestens ein«) sind dabei ebenso mit im Spiel wie Allquantoren (»alle«). Um notwendige und hinreichende Bedingungen miteinander zu verbinden, führte Zuse einen eigenen Formalismus ein: Die Verknüpfung von notwendigen Bedingungen stellt er fortan in Form von Reihen-schaltungen dar, jene von hinreichenden als Parallelschaltungen.
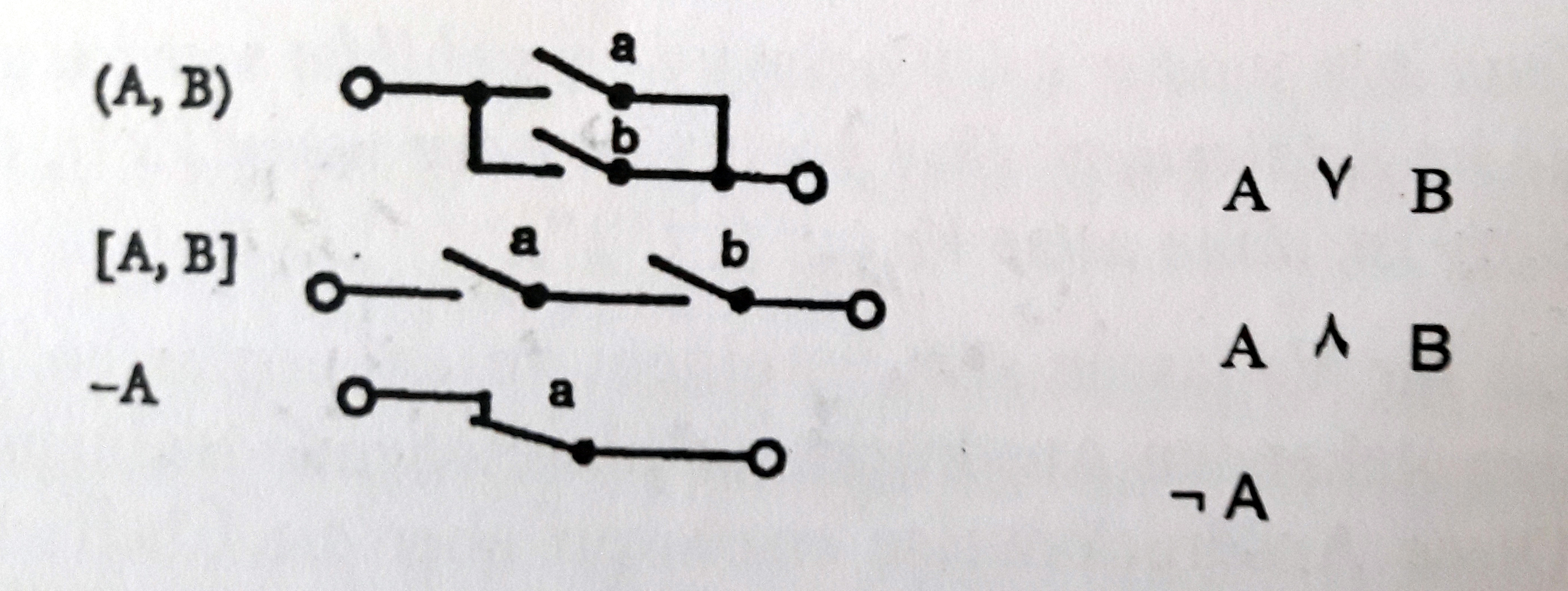
Schaltglieder als Logikformalismus (Bild: Barbara Eder)
»Plankalkül« ist eine auf logischen Universalia aufgebaute Programmiersprache, gemacht für die Z4. Als Datentypen gibt es Dezimalzahlen mit Exponenten, Integer – also ganze Zahlen ohne Nachstellenkomma –, Bool’sche Werte (z. B. wahr/falsch) und Binärziffern, angeordnet in Zahlenpaaren, Reihen oder Tupeln. Am linken Rand zu jeder Anweisung findet sich eine Art Metakommentar, die Buchstaben V, K und S sind dort in vertikaler Abfolge zu finden. Dabei handelt es sich um Abkürzungen, die für Datenstruktur (S), Komponentenzeile (K) oder Indexzeile (V) stehen; die Hauptzeile beinhaltet die zu berechnende Formel, während die Strukturzeile S für die Ausführung des Programms nicht zwingend notwendig ist und als Dokumentation zum Geschehen verstanden werden kann; die Strukturzeichen τ und σ fungieren indes als eine Art »numerischer Freiraum«: Sie stehen für beliebige Variablen und lassen sich in Form einer Paarliste oder als Matrix darstellen.
Die Idee hinter Zuses Programmiersprache »Plankalkül« ist mehr als zwei Jahrhunderte alt und lässt sich bis zu den (antiken) Anfängen des Werkzeuggebrauchs zurückverfolgen; erste Ansätze zur ihrer Formalisierung begannen mit der Weiterentwicklung mechanischer Uhrwerke im 17. Jahrhundert und kulminierten in Gottfried Wilhelm Leibniz’ Versuch einer formelhaften Reanimation der Apparate-Welt: Leibniz betrachtete wissenschaftliche Begriffe als allgemeine Zeichen innerhalb einer festgelegten Abfolge, die das Potenzial zur schematischen – und damit auch zur abstrakt-vereinfachenden – Darstellungen von Ideen beinhalten; er wollte seine mathesis universalis auch als allgemeine Zeichenlehre verstanden wissen, mit deren Hilfe man logisches Schließen automatisieren könne. Nicht zuletzt trüge dies zu einer Entlastung menschlicher Köpfe bei – ein auch für Konrad Zuse ausschlaggebender Impetus: Als Bauingenieur jahrelang in Rechenbüros geknechtet, begann Zuse von der maschinellen Automatisierung der eigenen Arbeitsleistung zu träumen. Der Gedanke an einen Formalismus, mithilfe dessen sich alle Berechnungen standardisieren ließen, stand am Beginn seiner Überlegungen.
»Zu den Pionieren zähle ich mich unbedingt, ich habe aber auch nichts dagegen, dass Sie mich als Erfinder des Computers bezeichnen, solange Sie sich im klaren sind, dass ich nicht der einzige bin; da gibt es natürlich neben mir noch mehr, ich hatte nur das Glück, dass meiner zuerst lief.« Mit diesen Worten gab Zuse wenige Jahre vor seinem Tod Auskunft darüber, ob ihm die Erfindung des ersten Computers realiter zuzuschreiben sei; sie wirkt ebenso bescheiden wie die Bedeutung, die er seinen Z-Maschinen zeitlebens beigemessen hatte. Zwar nannte er sie sein »Lebenswerk«, überschätzte ihre Funktion und Arbeitsleistung aber nicht. Zuses Ansicht nach sollten Computer stets so programmiert sein, dass sie menschliche Nutzer_innen bei der Ausführung bestimmter Aufgaben optimal unterstützen. Anders als die Prophet_innen der KI maßte er sich nicht an, seinen Maschinen Geist, Denken oder Bewusstsein einzuhauchen. Er begnügte sich stattdessen damit, seinem »mechanischen Gehirn« das Rechnen beizubringen – ganz im Sinne mathematischer Kalküle. Die damit einhergehende Befreiung des Kopfes von zu vielen Formeln schuf auch in seinem Fall Raum für Neues: Als Kuno See malte Zuse in seinen letzten Lebensjahren ganz unmetaphorisch Wolken auf Papier.

Plankalkül Programmierbeispiel in Zuses Handschrift (Bild: Barbara Eder)
Bezeichnet hat Zuse sich mitunter als »verträumter Pennäler, Bummelstudent, verhinderter Künstler, Maurer, Computer-Bastler, gescheiterter Unternehmer, Professor ohne Honorar, Büttenredner, verkannter Weltverbesserer, überspannter Erfinder, abgeklärter Philosoph«; jene erweiterbare Ansammlung an Tätigkeiten, die nicht immer Brot brachten, erscheint vor dem Hintergrund seines Denkens wie eine Liste von endlich vielen, aber nicht notwendigerweise voneinander verschiedenen Objekten; allen Elementen dieses Tupels scheint gemein, dass sie ein außerordentlich scharfes Denken erfordern. Zuse hat es im Zuge des Studiums eines Teilgebiets der Mathematik erworben, das zugleich zur Philosophie gehört; den analytischen Sirenengesängen aus Amerika ist die Logik bislang ebenso wenig erlegen wie ihren pragmatischen Pendants aus England; als intensive Form der Subjektivierung, die jede mathematische Beweisführung mit sich bringt, könnte sie der Philosophie jenes Differenzierungsvermögen zurückgeben, das Zuses frühen Computer-Architekturen zugrunde liegt.
